Chuyên đề Phương pháp toạ độ trong mặt phẳng | Chân trời sáng tạo Toán lớp 10

Mời các em cùng theo dõi bài học hôm nay với tiêu đề
Chuyên đề Phương pháp toạ độ trong mặt phẳng | Chân trời sáng tạo Toán lớp 10

Tài liệu chuyên đề Phương pháp toạ độ trong mặt phẳng Toán lớp 10 sách Chân trời sáng tạo gồm lý thuyết và các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán 10. 

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 10 Chân trời sáng tạo word có lời giải chi tiết:

Bạn đang xem: Chuyên đề Phương pháp toạ độ trong mặt phẳng | Chân trời sáng tạo Toán lớp 10

B1: Gửi phí vào tài khoản0711000255837 – NGUYEN THANH TUYEN – Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official – nhấn vào đây

Xem thử tài liệu tại đây: Link tài liệu

Chuyên đề Phương pháp toạ độ trong mặt phẳng

Tài liệu gồm 6 Chuyên đề nhỏ, mời bạn đọc xem thử nội dung Chuyên đề Đường thẳng :

Chuyên đề 2: ĐƯỜNG THẲNG

1. PHƯƠNG TRÌNH ĐƯỜNG THẲNG

a. Véc tơ chỉ phương và vectơ pháp tuyến của đường thẳng

– Vectơ \(\overrightarrow u  \ne \overrightarrow 0 \)được gọi là vectơ chỉ phương (VTCP) của đường thẳng \(\Delta \) nếu giá của nó song song hoặc trùng với \(\Delta \).

Nhận xét:

+ Nếu \(\overrightarrow u \) là một vtcp của đường thẳng \(d\) thì \(k.\overrightarrow u \,\,,\,\,\left( {k \ne 0} \right)\) cũng là một véc tơ chỉ phương của \(d\).

+ Một đường thẳng xác định khi biết một vtcp và một điểm mà nó đi qua.

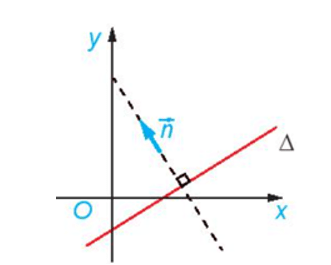
– Vectơ \(\overrightarrow n  \ne \overrightarrow 0 \) gọi là vectơ pháp tuyến (VTPT) của \(\Delta \) nếu giá của nó vuông góc với \(\Delta \).

Nhận xét:

a) Nếu \(\overrightarrow n \) là một vtpt của đường thẳng \(d\) thì \(k.\overrightarrow n \,\,,\,\,\left( {k \ne 0} \right)\) cũng là một vtpt của\(d\).

b) Nếu \(\overrightarrow n \) là một VTPT của đường thẳng \(d\) và \(\overrightarrow u \) là một VTCP của đường thẳng \(d\) thì \(\overrightarrow n .\overrightarrow u  = 0\).

c) Một đường thẳng xác định khi biết một VTPT và mộ điểm nó đi qua.

LIÊN HỆ GIỮA VTCP VÀ VTPT

1. Từ nhận xét “Nếu \(\overrightarrow n \) là một VTPT của đường thẳng \(d\) và \(\overrightarrow u \) là một VTCP của đường thẳng \(d\) thì \(\overrightarrow n .\overrightarrow u  = 0\)” ta rút ra được: nếu \(\overrightarrow n  = \left( {A;B} \right)\) là một VTPT của đường thẳng \(d\) thì một VTCP của \(d\) là \(\overrightarrow u  = \left( {B; – A} \right)\) ( hoặc \(\overrightarrow u  = \left( { – B;A} \right)\)).

2. Từ nhận xét “Nếu \(\overrightarrow n \) là một VTPT của đường thẳng \(d\) và \(\overrightarrow u \) là một VTCP của đường thẳng \(d\) thì \(\overrightarrow n .\overrightarrow u  = 0\)” ta rút ra được: nếu \(\overrightarrow u  = \left( {a;b} \right)\) là một VTCP của đường thẳng \(d\) thì một VTPT của \(d\) là \(\overrightarrow n  = \left( { – b;a} \right)\) (hoặc \(\overrightarrow n  = \left( {b; – a} \right)\)).

Hai nhận xét trên giúp ích rất nhiều trong việc chuyển đổi qua lại giữa các dạng phương trình đường thẳng. Từ PTTQ ta có thể chuyển sang PTTS và ngược lại.

b. Phương trình tham số của đường thẳng

Cho đường thẳng \(\Delta \) đi qua điểm \(A\left( {{x_0};{y_0}} \right)\)và có vectơ chỉ phương \(\overrightarrow u \left( {a;b} \right)\). Khi đó điểm \(M\left( {x;y} \right)\)thuộc đường thẳng \(\Delta \) khi và chỉ khi tồn tại số thực \[t\] sao cho \(\overrightarrow {AM}  = t\overrightarrow u \), hay

\(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\)          (2)

Hệ (2) được gọi là phương trình tham số của đường thẳng\(\Delta \) (t là tham số).

Đường thẳng \(d\) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) và có vtcp \(\overrightarrow u  = \left( {a;b} \right)\) thì có phương trình tham số là \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\). ( Mỗi điểm \(M\) bất kỳ thuộc đường thẳng \(\left( d \right)\) tương ứng với duy nhất một số thực \(t \in \mathbb{R}\) và ngược lại).

Nhận xét‎‎‎‎ :\(A \in \Delta  \Leftrightarrow A({x_0} + at;{y_0} + bt),t \in \mathbb{R}\)

Trong mặt phẳng với hệ tọa độ \[Oxy\], mọi phương trình dạng \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\) với \({a^2} + {b^2} \ne 0\) đều là phương trình của đường thẳng \(d\) có một vtcp là \(\overrightarrow u  = \left( {a;b} \right)\).

b. Phương trình tổng quát (PTTQ) của đường thẳng

Trong mặt phẳng tọa độ, mọi đường thẳng đều có phương trình tổng quát dạng \(ax + by + c = 0\), với \(a\) và \(b\) không đồng thời bằng \(0\). Ngược lại, mỗi phương trình dạng \(ax + by + c = 0\), với \(a\) và \(b\)không đồng thời bằng \(0\), đều là phương trình của một đường thẳng, nhận \(\overrightarrow n \left( {a;b} \right)\)là một vectơ pháp tuyến.

1. Đường thẳng \(d\) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) và có VTPT \(\overrightarrow n  = \left( {A;B} \right)\) thì có phương trình tổng quát là \(A\left( {x – {x_0}} \right) + B\left( {y – {y_0}} \right) = 0\).

2. Ngược lại, trong mặt phẳng với hệ tọa độ \(Oxy\) mọi phương trình dạng \[Ax + By + C = 0\left( {{A^2} + {B^2} \ne 0} \right)\] đều là phương trình tổng quát của đường thẳng \(d\) có VTPT \(\overrightarrow n  = \left( {A;B} \right)\).

3. Một số trường hợp đặc biệt của PTTQ\[Ax + By + C = 0\left( {{A^2} + {B^2} \ne 0} \right)\].

a) Nếu \(A = 0\) phương trình trở thành \[By + C = 0 \Leftrightarrow y =  – \frac{C}{B}\] đường thẳng song song với trục hoành \(Ox\) và cắt trục tung \(Oy\) tại điểm \(M\left( {0; – \frac{C}{B}} \right)\).

b) Nếu \(B = 0\) phương trình trở thành \(Ax + C = 0 \Leftrightarrow x =  – \frac{C}{A}\) đường thẳng song song với trục tung \(Oy\) và cắt trục hoành \(Ox\) tại \(M\left( { – \frac{C}{A};0} \right)\).

c) Nếu \(C = 0\) phương trình trở thành \[Ax + By = 0\] đường thẳng đi qua gốc tọa độ \(O\left( {0;0} \right)\).

d) Đường thẳng có dạng \(y = ax + b\), (trong đó \(a\) được gọi là hệ số góc của đường thẳng ) có VTPT là \(\overrightarrow n  = \left( {a; – 1} \right)\). Ngược lại đường thẳng có VTPT \(\overrightarrow n  = \left( {A;B} \right)\) thì có hệ số góc là \( – \frac{A}{B}\).

e) Đường thẳng \(d\) đi qua điểm \(A\left( {a;0} \right)\) và \(B\left( {0;b} \right)\) có phương trình là \(\frac{x}{a} + \frac{y}{b} = 1.\)

d. Phương trình chính tắc của đường thẳng

Đường thẳng \(d\) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) và có vtcp \(\overrightarrow u  = \left( {a;b} \right)\) với \(a \ne 0,\,b \ne 0\) có phương trình chính tắc là: \(\frac{{x – {x_0}}}{a} = \frac{{y – {y_0}}}{b}\)

Ví dụ: Viết phương trình tham số và phương trình tổng quát của đường thẳng d trong các

trường hợp sau:

a) Đường thẳng d đi qua điểm A(2; 1) và có vectơ chỉ phương \(\vec u\) = (3; 2);

b) Đường thẳng d đi qua điểm B(3; 3) và có vectơ pháp tuyển \(\vec n\) = (5; -2);

c) Đường thẳng d đi qua hai điểm C(1; 1), D(3;5).

Giải

a) Đường thẳng d đi qua điểm A(2; 1) và có vectơ chỉ phương \(\vec u\) = (3; 2), nên ta có phương trình tham số của d là:

\(\left\{ {\begin{array}{*{20}{c}}{x = 2 + 3t}\\{y = 1 + 2t}\end{array}} \right.\).

blog hotrohoctap.com

Đường thẳng d có vectơ chỉ phương \(\vec u\) = (3; 2) nên có vectơ pháp tuyền \(\vec n\) = (2; -3).

Phương trình tổng quát của d là: 2(x – 2) – 3(y – 1) = 0 ó 2x – 3y – 1 = 0.

b) Đường thẳng d có vectơ pháp tuyến \(\vec n\) = (5; -2) nên có vectơ chỉ phương \(\vec u\) = (2; 5).

Phương trình tham số của d là:

                                                     \(\left\{ {\begin{array}{*{20}{c}}{x\; = \;3 + 2t}\\{y\; = \;3 + 5t}\end{array}} \right.\).

Phương trình tổng quát của d là: 5(x – 3) – 2(y – 3) = 0 ó 5x – 2y – 9 = 0.

c) Đường thẳng d đi qua hai điểm C(1; 1),D(3; 5) nên có vectơ chỉ phương \(\vec u\) = \(\overrightarrow {CD} \) = (2; 4)

và có vectơ pháp tuyến \(\vec n\) = (4; -2).

Phương trình tham số của d là:  \(\left\{ {\begin{array}{*{20}{c}}{x\; = \;1 + 2t}\\{y\; = \;1 + \;4t}\end{array}} \right.\).

Phương trình tổng quát của d là:

4(x – 1) – 2(y – 1) = 0 ó 4x – 2y – 2 = 0 ó 2x – y – 1 =0

2. VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG

Trong mặt phẳng với hệ tọa độ \(Oxy\), cho hai đường thẳng \({d_1}:{a_1}x + {b_1}y + {c_1} = 0\) và \({d_2}:{a_2}x + {b_2}y + {c_2} = 0\).

Nếu \(\vec n\)₁ và \(\vec n\)₂ cùng phương thì ₁ và ₂ song song hoặc trùng nhau. Lấy một điểm P tuỳ ý trên ₁.

·          Nếu P \( \in \) ₂ thì ₁\( \equiv \) ₂.

·          Nếu P \( \notin \) ₂ thì ₁// ₂.

Nếu \(\vec n\)₁ và \(\vec n\)₂ không cùng phương thì ₁ và ₂ cắt nhau tại một điểm M(x₀; y₀) với (x₀; y₀) là nghiệm của hệ phương trình:

\(\left\{ {\begin{array}{*{20}{c}}{{a_1}x + {b_1}y + {c_1} = 0\;}\\{{a_2}x + {b_2}y + {c_2} = 0}\end{array}} \right.\).

Chú ý 1:

a) Nếu \(\vec n\)₁ . \(\vec n\)₂ = 0 thì \(\vec n\)₁ \( \bot \) \(\vec n\)_2, suy ra ₁\( \bot \) ₂.

b) Đề xét hai vectơ \(\vec n\)₁ (a₁; b₁) và \(\vec n\)₂ (a₂; b₂) cùng phương hay không cùng phương, ta xét biểu thức a₁b₁ – a₂b₂:

·          Nếu a₁b₁ – a₂b₂ = 0 thì hai vectơ cùng phương.

·           Nếu a₁b₁ – a₂b₂ \( \ne \) 0 thì hai vectơ không cùng phương.

Chú ý 2: Trong mặt phẳng với hệ tọa độ \(Oxy\), cho hai đường thẳng \({d_1}:{a_1}x + {b_1}y + {c_1} = 0\) và \({d_2}:{a_2}x + {b_2}y + {c_2} = 0\).

Để xét vị trí tương đối của hai đường thẳng này ta xét số nghiệm của hệ phương trình \(\left\{ \begin{array}{l}{a_1}x + {b_1}y + {c_1} = 0\\{a_2}x + {b_2}y + {c_2} = 0\end{array} \right.\)

+ Nếu hệ \(\left( {1.1} \right)\) có duy nhất 1 nghiệm ta nói hai đường thẳng trên cắt nhau tọa độ giao điểm chính là nghiệm của hệ phương trình nói trên.

+ Nếu hệ \(\left( {1.1} \right)\) vô nghiệm ta nói hai đường thẳng nói trên song song với nhau.

+ Nếu hệ \(\left( {1.1} \right)\)nghiệm đúng với mọi \(x \in \mathbb{R}\) thì hai đường thẳng trên trùng nhau.

+ Tuy nhiên để thuận tiện cho việc xét nhanh vị trí tương đối của hai đường thẳng ta chú ý nhận xét sau

Nhận xét. Nếu \({a_2}{b_2}{c_2} \ne 0\) ta có

a) \(\frac{{{a_1}}}{{{a_2}}} \ne \frac{{{b_1}}}{{{b_2}}} \Leftrightarrow {d_1} \cap {d_2} = \left\{ I \right\}\)

b) \(\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}}}{{{c_2}}} \Leftrightarrow {d_1}//{d_2}\)

c) \(\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}} \Leftrightarrow {d_1} \equiv {d_2}\)

3. GÓC GIỮA HAI ĐƯỜNG THẲNG

Trong mặt phẳng với hệ tọa độ \(Oxy\), cho hai đường thẳng \({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) và \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\).

Khái niệm góc giữa hai đường thẳng

Hai đường thẳng ₁ và ₂ cắt nhau tạo thành bốn góc.

·          Nếu ₁ không vuông góc với ₂ thì góc nhọn trong bốn góc đó được gọi là góc giữa hai đường thẳng ₁ và ₂.

·          Nếu ₁ vuông góc với ₂ thì ta nói góc giữa ₁ và ₂ bằng 90⁰.

Ta quy ước: Nếu ₁ và ₂ song song hoặc trùng nhau thì góc giữa ₁ và ₂ bằng 0⁰. Như vậy góc \(\alpha \) giữa hai đường thẳng luôn thoả mãn: 0⁰\( \le \) \(\alpha \) \( \le \) 90⁰.

Góc giữa hai đường thẳng ₁ và ₂ được kí hiệu là ( ) hoặc (₁, ₂).

Khi hai đường thẳng cắt nhau góc giữa hai đường thẳng được tính theo công thức:

\[\cos \left( {{\Delta _1};{\Delta _2}} \right) = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} \sqrt {a_2^2 + b_2^2} }}\]

4. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT ĐƯỜNG THẲNG

Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường thẳng \(\Delta :ax + by + c = 0\) và điểm \({M_0}\left( {{x_0};{y_0}} \right)\). Khi đó khoảng cách từ điểm \({M_0}\) đến đường thẳng \(\Delta \) được tính theo công thức:

\(d\left( {{M_0};\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)

 

Câu 1. Trong mặt phẳng tọa độ, cho  \(\overrightarrow n  = \left( {2;1} \right),\,\overrightarrow v  = \left( {3;2} \right),\,A\left( {1;3} \right),\,B\left( { – 2;1} \right).\)

a) Lập phương trình tổng quát của đường thẳng \({\Delta _1}\) đi qua \(A\) và có vectơ pháp tuyến \(\overrightarrow n .\)

b) Lập phương trình tham số của đường thẳng \({\Delta _2}\) đi qua \(B\) và có vectơ chỉ phương \(\overrightarrow v .\)

c) Lập phương trình tham số của đường thẳng \(AB.\)

Câu 2. Lập phương trình tổng quát của các trục tọa độ.

Câu 3. Cho hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 + 5t\end{array} \right.\) và \({\Delta _2}:\,2x + 3y – 5 = 0.\)

a) Lập phương trình tổng quát của \({\Delta _1}.\) b) Lập phương trình tham số của \({\Delta _2}.\)

Câu 4. Trong mặt phẳng tọa độ, cho tam giác \(ABC\) có \(A\left( {1;2} \right),\,B\left( {3;0} \right)\) và \(C\left( { – 2; – 1} \right).\)

a) Lập phương trình đường cao kẻ từ \(A.\)           b) Lập phương trình đường trung tuyến kẻ từ \(B.\)

Câu 5. (Phương trình đọan chắn của đường thẳng )

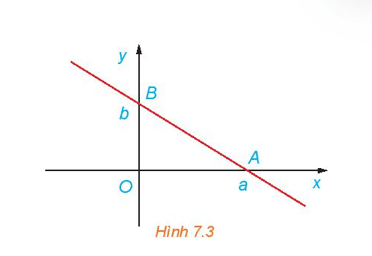
Chứng minh rằng, đường thẳng đi qua hai điểm \(A\left( {a;0} \right),\,B\left( {0;b} \right)\) với \(ab \ne 0\,\left( {H.7.3} \right)\) có phương trình là: \(\frac{x}{a} + \frac{y}{b} = 1.\)

Câu 6. Theo Google Maps, sân bay Nội Bài có vĩ độ là \(21,2{}^0\) Bắc, kinh độ \(105,8{}^0\)Đông, sân bay Đà Nẵng có vĩ độ là \(16,1{}^0\) Bắc, kinh độ \(108,2{}^0\)Đông. Một máy bay, bay từ Nội Bài đến sân bay Đà Nẵng. Tại thời điểm  \(t\) giờ, tính từ lúc xuất phát, máy bay ở vị trí có vĩ độ \(x{}^0\) Bắc, kinh độ \(y{}^0\)Đông được tính theo công thức

\(\left\{ \begin{array}{l}x = 21,2 – \frac{{153}}{{40}}t\\y = 105,8 + \frac{9}{5}t\end{array} \right.\)

a) Hỏi chuyến từ Hà Nội đến Đà Nẵng mất mấy giờ?

b) Tại thời điểm \(1\) giờ kể từ lúc cất cánh, máy bay đã bay qua vĩ tuyến \(17\) (\(17{}^0\) Bắc) chưa?

Câu 7.  Xét vị trí tương đối giữa các cặp đường thẳng sau:

a) \[{\Delta _1}:3\sqrt 2 x + \sqrt 2 y – \sqrt 3  = 0\] và \[{\Delta _2}:6x + 2y – \sqrt 6  = 0\].

b) \[{d_1}:x – \sqrt 3 y + 2 = 0\] và \[{d_2}:\sqrt 3 x – 3y + 2 = 0\].

c) \[{m_1}:x – 2y + 1 = 0\] và \[{m_2}:3x + y – 2 = 0\].

Câu 8.  Tính góc giữa các cặp đường thẳng sau:

a) \[{\Delta _1}:\sqrt 3 x + y – 4 = 0\] và \[{\Delta _2}:x + \sqrt 3 y + 3 = 0\].

b) \[{d_1}:\left\{ {\begin{array}{*{20}{c}}{x =  – 1 + 2t}\\{y = 3 + 4t}\end{array}} \right.\] và \[{d_2}:\left\{ {\begin{array}{*{20}{c}}{x = 3 + s}\\{y = 1 – 3{\rm{s}}}\end{array}} \right.\] (\[t,{\rm{ }}s\]là các tham số).

Câu 9. Trong mặt phẳng toạ độ \[Oxy\], cho điểm \[A\left( {0; – 2} \right)\]và  đường thẳng  \[\Delta 😡 + y – 4 = 0\].

a) Tính khoảng cách từ điểm  \[A\] đến đường thẳng \[\Delta \].

b) Viết phương trình đường thẳng \[a\] đi qua điểm \[M\left( { – 1;0} \right)\] và song song với \[\Delta \].

c) Viết phương trình đường thẳng \[b\] đi qua điểm \[N\left( {0;3} \right)\] và vuông góc với \[\Delta \].

Câu 10.  Trong mặt phẳng toạ độ, cho tam giác \[ABC\] có \[A\left( {1;0} \right),{\rm{ B}}\left( {3;2} \right)\] và \[{\rm{ C}}\left( { – 2; – 1} \right)\].

a) Tính độ dài đường cao kẻ từ đỉnh \[A\] của tam giác \[ABC\].

b) Tính diện tích tam giác \[ABC\].

Câu 11. Chứng minh rằng hai đường thẳng \[d:y = ax + b{\rm{ }}\left( {a \ne 0} \right)\] và \[d’:y = a’x + b'{\rm{ }}\left( {a’ \ne 0} \right)\] vuông góc với nhau khi và chỉ khi \[aa’ =  – 1\].

Câu 12. Trong mặt phẳng toạ độ, một tín hiệu âm thanh phát đi từ một vị trí và được ba thiết bị ghi tín hiệu đặt tại ba vị trí \[O\left( {0;0} \right),{\rm{ }}A\left( {1;0} \right),{\rm{ B}}\left( {1;3} \right)\] nhận được cùng một thời điểm. Hãy xác định vị trí phát tín hiệu âm thanh.

 

 

Trên đây là toàn bộ nội dung về bài học
Chuyên đề Phương pháp toạ độ trong mặt phẳng | Chân trời sáng tạo Toán lớp 10
. Hy vọng sẽ là tài liệu hữu ích giúp các em hoàn thành tốt bài tập của mình.

Đăng bởi: https://thcslequydoncaugiay.edu.vn/

Chuyên mục: Tài Liệu Học Tập